How do ratio pyrometers work?
A pyrometer is a type of thermal sensor used for measuring high temperatures of a surface, often in large furnaces or kilns. These devices measure the temperature of an object or surface from the thermal radiation emitted, also known as radiometry. There are many applications where a standard one-color pyrometer reads the temperature incorrectly and they include:
- Small objects (too small to fill the cone-of-vision).
- Dust, smoke or steam which obscures the line of sight.
- Windows in the process that get dirty and are difficult to keep clean.
- Emissivity of the product changes (due to change in alloy or surface condition).
A two-color or ratio pyrometer, such as Endurance Series, can operate properly even with these problems and indicate the correct temperature.
What is different about a two-color pyrometer versus a one-color pyrometer? A two-color pyrometer consists of two one-color pyrometers in the same package. It uses two detectors, operating at two separate wavelengths, but both detectors see the same hot target.
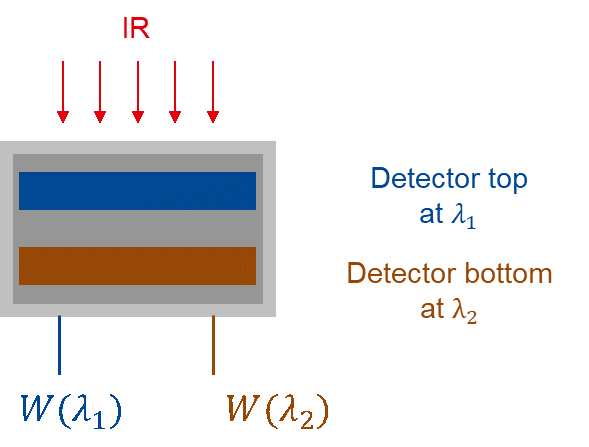
Implementation scheme for a ratio pyrometer using 2 detectors in a sandwich structure
No Signal Attenuation
Let’s first consider the blue graph in the example below. The two-color thermometer is looking at a blackbody with an emissivity value of 1.0 and a blackbody temperature of 1500°C. Based on the Planck law, the two detectors are providing the following energy units in accordance to the blue curve at an emissivity value of 1.0:
Detector #1 at wavelength λ1 will give an output of 500 units.
Detector #2 at different wavelength λ2 will output a signal of 1000 units.
Since this is a ratio thermometer, we divide 1000 by 500 and get a ratio of 2. The instrument is calibrated in a way to read 1500°C when it sees a ratio of 2.
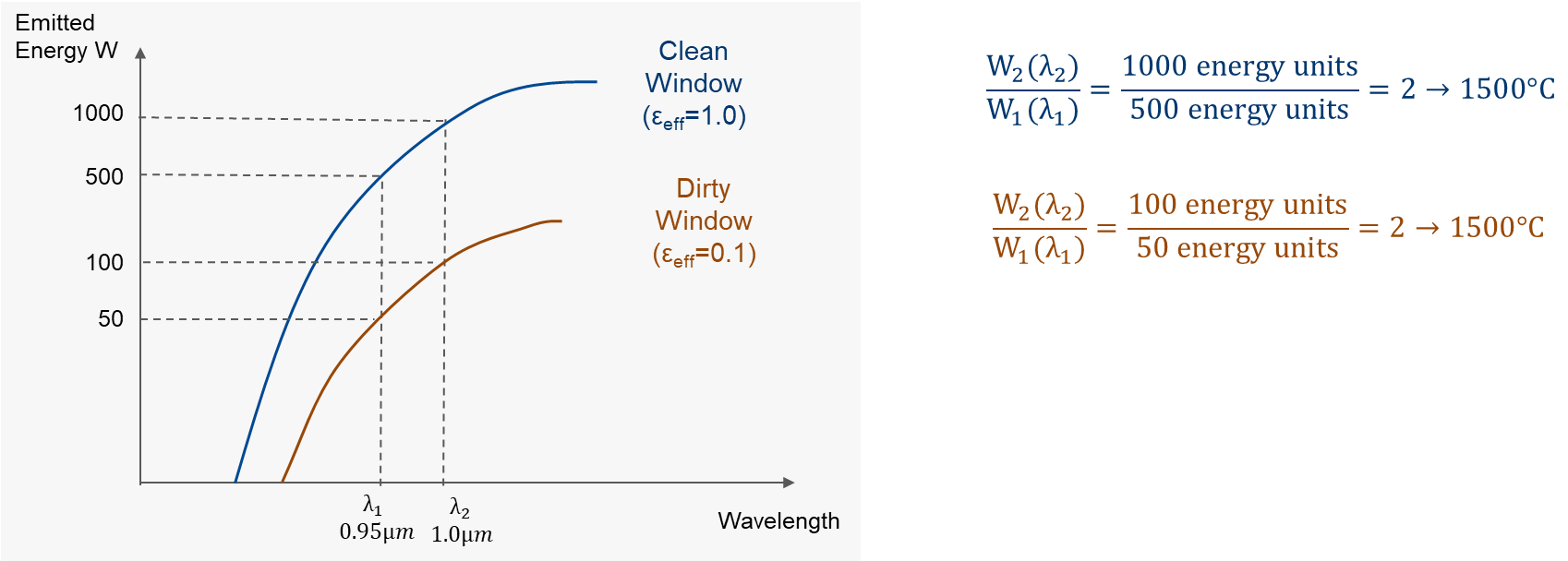
Planck curves for the ratio thermometer looking with two detectors at a blackbody at a temperature of 1500°C
Signal Attenuation
Now what happens if somehow the signal from the hot target is reduced or prevented from getting to the detector? This could be caused by a dirty window, object too small to fill the cone-of-vision, or maybe there is smoke in the line of sight. The brown graph depicts an example with a 90% signal loss, but the target temperature is still 1500°C. This is the same as having the apparent emissivity drop from 1.0 to 0.1.
Detector #1 will output a signal of 50 units.
Detector #2 will output a signal of 100 units.
Both signals have been reduced by 90% as compared to the upper curve (E=1.0). Note that 100 divided by 50 is again a ratio of 2, or the instrument will read 1500°C even though we have lost 90% of the signal. Every two-color thermometer has a limit as to how much signal can be reduced. This is called the attenuation which can vary from 0% to as high as 95% of the signal and still read an accurate temperature.
E-Slope
Basically, a two-color thermometer works properly as long as whatever affects one wavelength, must affect the other wavelength the same amount. Unfortunately, there are applications where the object emissivity is different for the two wavelengths for example measuring molten metals. When the two-color thermometer looks at the molten metal, the signal ratio (or slope) will be incorrect and an error will occur in the temperature reading.
How can this be corrected? All two-color thermometers have an adjustment called E-Slope. When viewing the molten metal, the E-Slope adjustment is turned until the instrument reads the correct metal temperature. The correct temperature may be obtained by using a disposable thermocouple. This E-Slope adjustment simply corrects the ratio by a constant which corrects the instrument indication for the unequal spectral emissivities of the target. Once the E-Slope is adjusted, then the problems of smoke, steam, dust, small targets, etc., are handled correctly by the instrument.